Pour la plupart, elles sont gratuites (celles présentées ici le sont) et vous permettent de réaliser de nombreuses tâches mathématiques en ligne. Il y aussi des applications destinées aux plus petits et des jeux mathématiques et logiques. Vous pouvez donc faire, sans dépenser d'argent, votre marché (de Noël) sur Chrome Web Store Education.

J'en ai sélectionné quelques unes qui me semblaient intéressantes , dans le cadre d'un usage pour l'enseignement en lycée et une publication en ligne, il y en a d'autres et j'en ai peut-être raté certaines intéressantes.

• Les grapheurs: Graph.tk et Desmos.

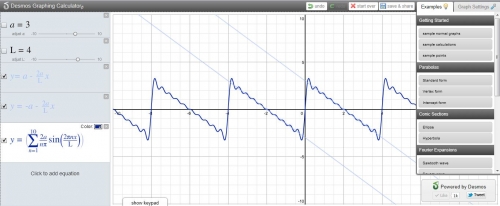
Je voulais faire un prochain billet sur Desmos Graphing Calculator (que l'on peut aussi trouver en ligne) et voilà que je le retrouve directement accessible dans  mon navigateur. Il permet de réaliser des graphiques en ligne, d'obtenir le fichier image ou l'adresse de la représentation pour la diffuser dans un billet de blog ou dans un message.

A noter:

La possibilité de représenter des développement de Taylor et des séries de Fourier

Le possibilité de définir des courbes de façon polaire

Les sections coniques définies de façon implicite

Le régionnement du plan

Graph.tk est du même type mais je ne suis pas parvenu  revenir dans l'éditeur après avoir demandé une image...

• L'éditeur d'équation Daum

Il permet de réaliser des écritures mathématiques de façon très fluide et rapide car les menus sont très simples et fournis. On peut ensuite demander un fichier image ou texte. Le code Latex est édité en même temps (il est un peut surprenant à l'oeil mais il s'agit du code correct lorsqu'on le copie dans le presse papier!

Voilà le résultat:

Le code Latex correspondant  est édité et il est utile par exemple, pour l'insérer dans GeoGebra.

• Les calculatrices.

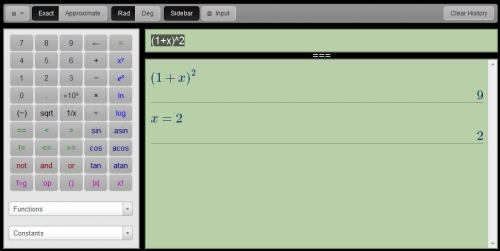
Je ne détaillerai pas cette partie, mais l'idée de retrouver directement une calculatrice scientifique dans un navigateur ne me parait pas inintéressante.

• Représentation de données.

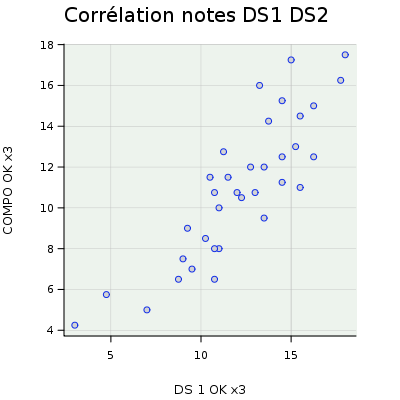
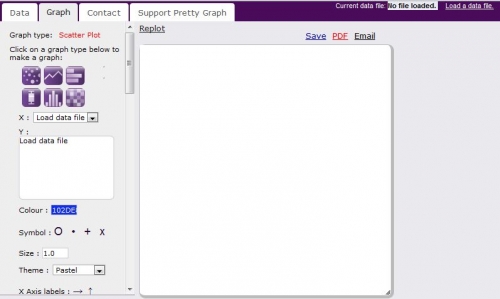
Pretty graph permet de télécharger un fichier excel, txt, csv ou dat et de représenter les données de façon rapide. On peut ensuite demander une image ou un fichier pdf. J'ai pris mon fichier de notes pour établir une corrélation sur les notes de deux devoirs sur tables, le premier en abscisses et le second en ordonnées:

Représentation de graphes.

Graph Drawer permet de représenter de façon rapide et simple (j'ai compris!!! donc c'est simple) des graphes 2D ou 3D.

• Attracteurs étranges

En passant j'ai récupéré une application ezFractal, représentant des attracteurs étranges. Il s'agit plus d'une exploration visuelle qu'autre chose:

Bon Noël et n'hésitez pas à me laisser une trace de votre marché dans Chrome Web Store si vous voyez des choses mathématiquement compatibles.

Une équipe de l'université de Padoue en Italie vient de mettre en évidence l'existence d'une corrélation entre la capacité à estimer un temps et l'intelligence mathématique. La corrélation n'est pas significative avec l'intelligence générale.

La source: Plos One

Le projet Exo7 propose aux étudiants des fiches d’exercices de mathématique avec indications et corrections de niveau L1/Math Sup, L2/Math Spé, L3/Licence. Ces fiches sont élaborées, corrigées et validées par des enseignants du supérieur.

Il contient aussi depuis peu des vidéos d'excellente qualité, de corrections d'exercices, visibles sur Youtube.

Sur MathemaTice

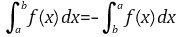
Au début du XXème siècle, Emile Borel, brillant mathématicien,  pronait le développement des laboratoires mathématiques dans les classes pour que les élèves se rendent compte qu'elles ne sont pas une pure abstraction... On a vu se pousuivre le développement des laboratoires de physique expérimentale et de SVT, mais pourquoi le système scolaire français n'a-t-il jamais poussé plus en avant cette idée?

Il semble que la valeur éducative de l’enseignement mathématique ne pourra qu’être augmentée si la théorie y est, le plus souvent possible, mêlée à la pratique. L’élève comprendra qu’il est sans doute excellent de bien raisonner, mais qu’un raisonnement juste ne conduit à des résultats exacts que si le point de départ est lui-même exact ; qu’il faut, par suite, ne pas croire aveuglément à tout raisonnement, à toute démonstration d’apparence scientifique, mais se dire toujours que la conclusion n’a de valeur qu’autant que les données ont été scrupuleusement vérifiées par l’expérience. C’est la meilleure éducation que nous pouvons souhaiter donner à nos élèves. Quand ils auront bien compris à la fois la puissance indéfinie du raisonnement abstrait et son incapacité absolue à créer de toutes pièces une vérité pratique, ils seront mieux armés pour la vie.

Le hasard, Emile Borel, éd. Librairie Félix Alcan, 1914, p. 12-13

On pourra lire avec un intérêt tout particulier la conférence qu'il a donné le 3 mars 1904 au  musée pédagogique d'où sont extraites les citations suivantes:

Mais pour amener, non seulement les élèves, mais aussi les professeurs, mais surtout l’esprit public à une notion plus exacte de ce que sont les Mathématiques et du rôle qu’elles jouent réellement dans la vie moderne, il sera nécessaire de faire plus et de créer de vrais laboratoires de Mathématiques.

Si la création de laboratoires en partie communs, se prêtant des appareils, utilisant même, dans un petit établissement, les mêmes outils, pouvait avoir pour résultat de rapprocher les physiciens et les mathématiciens, ce serait déjà une raison suffisante pour les créer.

j’ai parlé de ce que, à mon sens, il y avait à faire au point de vue des exercices pratiques de Mathématiques, mais je n’ai pas dit qu’il fallait supprimer l’enseignement théorique des Mathematiques ; je pense, au contraire, qu’on peut le conserver tel qu’il existe (à peu de chose près) ; mais cet enseignement théorique ne sera que mieux compris s’il est accompagné d’exercices pratiques, tels que nous avons essayé de les définir.

Cela étant bien entendu, il semble que la valeur éducative de l’enseignement mathématique ne pourra qu’etre augmentée si la théorie y est, le plus souvent possible, mélée à la pratique.

Les diagrammes suivants, bien que très usuels m'ont posé pas mal de difficultés pour les insérer dans une publication numérique. Entre solutions longues et parfois bancales, je jonglais plus ou moins habilement avec les logiciels dont je disposais et des copies d'écran pas toujours de bonne qualité.

Pour réaliser ces diagrammes, il suffit d'installer PstPlus  de le configurer correctement comme c'est expliqué. Attention, il faut indiquer pour Windows, le chemin de gswin32c.exe  et non de gswin32.exe associé à Ghostscript. Il faut aussi installer une distribution Latex.

Une fois ces opérations réalisées, on peut générer un fichier en .eps à partir des différents assistants.

Il suffit ensuite d'utiliser un convertisseur en ligne pour obtenir une image. Pour ma part j'ai utilisé epsconverter, très facile d'emploi.