Inclassables Mathématiques 2.0

La sculpture du Dieu du Zéro réalisée par mon père

Le zéro posa beaucoup de difficultés à l'humanité. Les égyptiens ne le connaissaient pas, les romains non plus. Les babyloniens utilisèrent un symbole  ( deux clous inclinés ) permettant de différencier 16 de 106 autrement qu'en écartant les  chiffres 1 et 6  ce qui indiquait dans le deuxième cas que la place des dizaines était vacante et qu'il fallait lire 106 et non 16 ( leur système était sexagésimal : base 60 => 3600,60,1 ainsi (106) = 1x3600+0x60+6x1=3636 en numération décimale) . Le zéro de position était né mais pas notre zéro ( celui de la tête à toto ). Les grecs en avaient tellement peur qu'ils en nièrent l'existence de peur de faire effondrer leur conception théologico-mathématico-philosophique. Admettre son existence c'est admettre l'existence du vide, du néant, et cela ne pouvait être compatible avec leur construction géométrique de l'univers et son harmonie. Son absence mis la pagaille jusque dans le calendrier. Souvenons-nous du vrai faux passage au 3ème millénaire en 2000 qui aurait du être fété en 2001 puisque l'année 0 n'est pas comptée ! Regardez où est notre pauvre 0 sur un clavier téléphonique , sur un pavé numérique, seul ou après le 9, jamais dans la suite 0, 1, 2,... mais heureusement il y eu les Mayas qui eurent un peu moins peur que tous les occidentaux réunis et ne freinèrent pas l'idée du 0 jusqu'au XVI ème siècle où la conception aristotélicienne du monde ( sans vide ) commença à sérieusement à s'effriter. Les Mayas  possédaient deux systèmes de numération, l'un fondé sur des points, des traits et sûrement des coquillages et l'autre, plus exotique et moins courante, basé sur des glyphes céphalomorphiques qu'ils écrivaient verticalement.

Les Mayas se préoccupaient beaucoup de la comptabilité des jours et des mois, ils connaissaient la numération de position et inventèrent le zéro. Ils  créèrent un système complexe de repérage temporel combinant le calendrier solaire et un calendrier rituel.  Chacun des glyphes numéroté de 1 à 13 était associé à une tête de divinité du monde supérieur. Par exemple le 5 était associé au dieu-Maïs, le 10 au dieu de la Mort ( on remarquera que sa machoire inférieure est rapportée ). Les glyphes numérotés de 14 à 19 ont été forgés à partir des glyphes 4 à 9 en décharnant leur machoire inférieure, l'opération constituait une règle arithmétique élémentaire puisque le dieu de la Mort ( 10) était symbolisé par un maxillaire inférieur.
Le dieu Zéro s'approche mais éloignons-nous un peu de lui auparavant.
En 1988, les fouilles entreprises à Teotihuacan à proximité de la pyramide de Quetzalcoalt ont mis à jour un grand nombre de tombes ainsi que les restes de 260 victimes sacrificiées lors de l'inauguration du monument dédié au serpent à plumes ( 150-200) assorties d'offrandes dont de nombreux maxillaires  supérieurs et des mandibules humains. Ces pratiques relevaient de la réactualisation d'anciens mythes. Xolotl est un dieu peint en noir et sur son pectoral figure un maxillaire inférieur humain décharné. Il représente la face nocturne de Quetzacoalt, son frère jumeau, sa personnalité chtonienne. C'est un être larvaire. Il avait la capacité de se dédoubler ce qui rendit son anéantissement difficile mais dès qu'il fut tué sous sa forme larvaire, le soleil se mit en mouvement. Un autre mythe le met en scène à  chaque coucher du soleil où se rejoue la bataille des dieux : Quetzalcoalt livre bataille contre les forces des ténèbres dans un jeu de balles divin ayant lieu à minuit. Les quatres protagonistes sont Quetzalcoalt le Dieu de l'aurore, le lune comme déesse mère, Xolotl comme dieu crépusculaire et le soleil comme victime sacrificielle. Xolotl gagne contre Quetzalcoalt et sacrifie le soleil, Quetzalcoalt s'unit à la déesse mère et de leur union nait chaque matin un nouveau soleil resplendissant : le dieu du maïs. C'est dans cet endroit maudit que les Jumeaux combattent éternellement pour que revive la lumière. Un des habitants de cet enfer symbolisait la mort par sacrifice : le dieu du chiffre zéro, il fut associé à un glyphe. 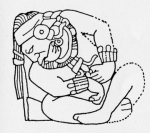Pour les mayas, la façon de transcrire les chiffres se fait verticalement, les plus grandes unités en haut, les plus petites en bas. Le zéro signifiait la fin, l'achèvement dont la main à la place de la machoire en témoigne. De par ses attributs, il s'impose comme le dieu de la mort sacrificielle qui patrone une forme de sacrifice particulièrement violent : l'arrachage de la machoire inférieure dont la main appliquée sur le glyphe semble ébaucher ce geste. On ne connait pas précisément l'origine de cette forme terrible de meurtre rituel mais il semblerait que l'arrachage de la mandibule inférieure résulte d'un mythe fondateur. 


Le fait que les mayas ne passèrent pas le cap de zéro algébrique fût du au fait que leur système de numération n'était pas tout à fait vigésimal c'est à dire en base vingt. En effet alors que l'on aurait dû trouver une écriture de nombres de trois chiffres sur la base 1, 20 et 20x20=400 : (111) = 1x400+1x20+1x1=421, leur système faisait intervenir la base 1, 20,  360  c'est à dire que (111) = 1x360+1x20+1x1=400, ce qui fit que 400 s'écrivait (120) et non (100) ôtant toute propriété algébrique au 0 !

Pour compléter : les Ecritures mayas du Nombre ( PDF ) : ICI

Pour en savoir plus :

Histoire universelle des chiffres Georges Ifrah

Zéro la biographie d'une idée dangeureuse Charles Seife

Revue de l'histoire des religions Les compagnons de l'enfer Jean-Claude Delhalle et Albert Luykx

Cliquer sur l'image pour accéder au musée de Cleveland

On reconnait sur la tête sculptée de ce jeune noble -?- , la main qui remplace la machoire inférieure.
                                 

Axiome 1 : ( Dichotomie ) Une propriété est vraie si et seulement si sa négation est fausse.
Axiome 2 : ( Fermeture ) Une propriété est vraie si elle contient nécessairement une propriété vraie.
Théorème 1 : Une propriété vraie est logiquement consistante ( i.e. il est possible de trouver au moins un exemple ).
Définition : Quelque chose est semblable à Dieu si et seulement si il contient toutes les propriétés vraies.
Axiome 3 : Etre semblable à Dieu est une propriété vraie.
Axiome 4 : Etre une propriété vraie est (logique, donc ) nécessaire.
Définition : Une propriété P est l'essence de x si et seulement si x possède P et P est nécessairement minimale.
Théorème 2 : Si x est semblable à Dieu, alors être semblable de Dieu est l'essence de x
Définition : NE(x): x existe nécessairement s'il a une propriété essentielle.
Axiome 5 : Etre NE est être semblable à Dieu
Théorème 3 : Il existe nécessairement x tel que x est semblable à Dieu.