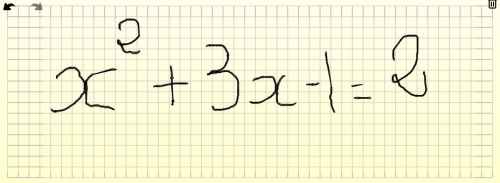Qui connait Edmodo? Réseau social sécurisé pour l'éducation
J'ai l'impression que dans le monde de l'éducation francophone, très peu d'enseignants connaissent Edmodo, un outil pourtant formidable que j'utilise pleinement.
Un excellent tutoriel a été réalisé par Laurence Bernard, de l'Académie de Martinique, dans le cadre des langues vivantes.
Laurence a de plus rédigé un article, faisant la synthèse d'une année d'utilisation, tout à fait positive.
Pour ma part je l'utilise depuis la rentrée 2009 et cette année tous mes élèves sont inscrits. On peut même y écrire des maths car Edmodo reconnait le Latex. Vous pouvez voir tous les articles que j'ai publiés sur le sujet pour vous convaincre de la puissance de cet outil. Il est possible consulter ICI la page de certains commentaires que j'ai rendus publics.
Je suis surpris du peu de publication (pour ne pas dire de l'absence) de publications francophones sur le sujet!
Il est à noter depuis la publication du tutoriel de Laurence que de nouvelles fonctionnalités ont été implémentées dans l'application (qui est disponible sur Smartphone d'ailleurs!).
Les principales nouveautés de cette version récente que j'utilise sont les suivantes:
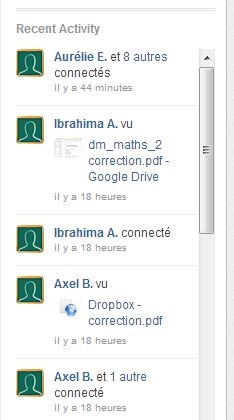
L'activité des élèves en direct:
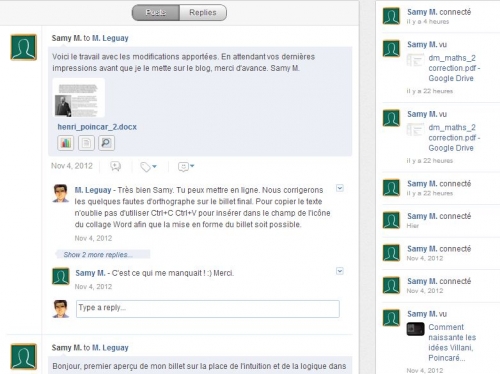
L'activité de chaque élève sur le réseau:
La possibilité de créer des sous-groupes: