Liens ministère, Sites académiques, IREM, APMEP
Le portail des sites académiques
Pour le prof de maths - Page 98
-
Le Portail des IREM -
Liens pédagogiques et scolaires
Euler - 1400 exercices en ligne de l'Académie de Versailles Mathenpoche - exercices collège-2nde
L'E-cureuil- Cours et animations de Lycée
Dynamaths - Logithèque - cours – exercices
Xmaths- Cours et exercices corrigés – Lycée
Abcmaths - Cours et exercices dynamiques de lycée
Espace élèves - exercices corrigés cours collège
Le Matou Matheux - Exercices primaire et collège
Maths Express - annales bac olympiades, concours général et corrigés
Dictionnaire mathématique de lycée
Forum et cours : L'île des mathématiques
Matematikos - des exercices niveau lycée
xm1 maths - Exercices et cours, 2ndes, premières, terminales
QCM de maths - 2ndes, 1ères ES et 1ères STG
Maths54 - cours, exercices et corrigés
Bacamaths - cours exercices 2ndes premières terminales
In f(x) Venenum - Mathématiques au lycée
Annuaire cours et sujets divers
Cours de mathématiques de Saint-Cyr + exercices corrigés
La taverne de l'Irlandais et Mathilde
Les cours du lycée Vincent d'Indy
Les exercices intéractifs de Lili pour la seconde
Les cours originaux de Téhessin le Rezéen ( terminale S )
Ecrire des maths ( pour profs )
St@tnet - cours sur les statistiques
mathématiques - Questions résolues
L'université en ligne ( 1 er cycle ) - Cours – exercices
Culture Maths - Culture générale
Maths en ligne - pour la seconde, évaluations et exercicesFiches de cours et devoirs Maths93
Aspect historiques
Math-O-Clic : QCM, méthodes, synthèses démonstrations pour Terminale SLes vidéos de cours de collège
Les pages mathématiques interactives avec Géoplan du Lycée Alain Borne
-
Le paradoxe de Bertrand
Paradoxe de la corde prise au hasard ( Bertrand )
Problème : On trace une corde au hasard dans un cercle. Quelle est la probabilité pour que sa longueur soit supérieure au côté du triangle équilatéral inscrit ?
Bertrand donne 3 solutions différentes à ce problème.
En vert les cordes possibles
En rouge les cordes impossibles
Première solution :
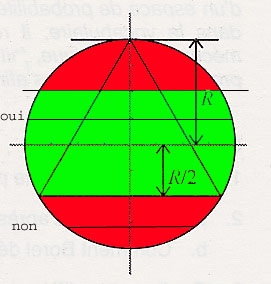
On peut pour des raisons de symétrie se donner la direction de la corde ; le point d'intersection de cette corde avec le diamètre ( vertical sur la figure ) perpendiculaire à cette direction devra alors se trouver sur un segment égal à la moitié de la longueur de ce diamètre ( car la distance au centre du côté du triangle équilatéral inscrit est égale à la moitié du rayon ) ; la probabilité est donc de 1/2.
Deuxième solution :
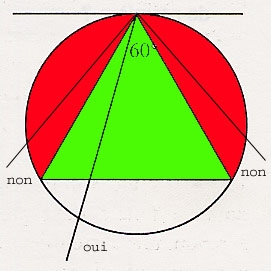
On peut, pour des raisons de symétrie, se donner une des extrémités de la corde sur le cercle ; la tangente en ce point et les 2 cotés du triangle équilatéral inscrit ayant ce point pour sommet forment trois angles de 60° ; la direction de la corde doit être à l'intérieur de l'angle formé par le triangle ( en vert) ; la probabilité est donc de 1/3.
Troisième solution :
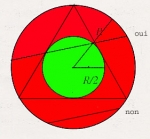
Pour fixer la position de la corde, il suffit de donner son milieu ; pour que la corde satisfasse à la condition de l'énoncé, il faut que son milieu soit intérieur à un cercle concentrique au cercle donné et de rayon moitié. La surface de ce cercle ( vert ) est le quart de la surface donnée ; la probabilité est donc de 1/4.
Doit-on penser que ces trois solutions sont également bonnes et, par suite, également mauvaises ? se demande Emile Borel dans son livre Le hasard parut en 1914. Nullement, poursuit-il, il s'agit simplement de préciser le mode d'après lequel se fera la vérification expérimentale, c'est à dire comment on s'y prendra pour tracer une corde au hasard : si on assujetit cette corde à passer par un point fixe du cercle ou si l'on fixe son milieu au hasard, il faudra choisir la deuxième ou la troisième solution, mais il est aisé de voir que la plupart des procédés naturels que l'on peut imaginer conduisent à la première.
Un site traite de ce "paradoxe" et permet la simulation des expériences : ICI
Un fichier pdf de Culturemath : ICI -
Tristes mathématiques
Turing ( père de l'informatique ) : suicide au cyanure certainement suite à un traitement chimique de son homosexualité
Gödel ( certainement le plus grand mathématicien du XXème siècle ): mort de faim
Lovelace ( première programmeuse ) : sa mère cacha la morphine pour obtenir la redemption de sa fille alors qu'elle mourrait d'un cancer
Cantor ( a étudié la notion d'infinis ) : meurt à l'hopital psychiatrique
Riemann ( père de l'intégration ): meurt à 39 ans
Hypatie ( néo-platonicienne, disciple de Pythagore ) : tuée par les chrétiens pour paganisme en lui arrachant la peau avec des coquilles d'huitres et ses membres furent livrés aux flammes.
-
Et pourtant elle tourne...
Ce n'est pas Copernic qui a découvert que la terre tournait autour du soleil mais bien avant lui : Aristarque de Samos