Un blog entièrement consacré à ce sujet : ICI

Quelques modèles mécaniques et électroniques : ICI

Et si vous ne saviez pas qu'un moulin à poivre pouvait faire des calculs, allez faire un tour  ICI  

L'histoire des calculatrices de poche : ICI

Le Musée de l'histoire de l'informatique : ICI

Voir aussi les machines mathématiques : ICI et l'article d'Interstices sur l'histoire du calcul numérique : ICI

Histoire du calcul par l'Institut International d'Informatique Léon Bollée : ICI

Schickard, l'inventeur de la première machine à calculer : ICI
La machine de Schickard : ICI
Quelques pages le concernant : ICI

L'article sur la machine à congruence du Musée des Arts et Métiers : ICI
Les machines pour explorer les nombres entiers de Lehmer les images : ICI

Un article sur la machine des frères Carissan ( PDF ) : ICI

Plus généralement, le site du Musée de l'histoire de l'ordinateur ( anglais ): ICI


Cette machine pour explorer les nombres entiers a été conçue en 1926 par Lehmer. Le dsipositif est rustique, il n'utilise qu'un chevalet, les chaines de bicyclette et d'autres outils ordinaires. C'était en fait un calculateur "spécialisé" que l'on pouvait programmer pour la recherche "rapide" des nombres ayant une forme spéciale. On peut programmer sur la machine un problème conduisant à une solution numérique en mettant des boulons dans certains maillons des chaines de bicyclette. Lorsqu'un moteur entraine les chaines, la machine tourne jusqu'à ce que tous les boulons soient alignés et la machine s'arrête alors automatiquement. Le nombre correspondant à la configuration des chaines au moment de l'arrêt satisfait les conditions imposées. Extrait de "Pour la Science" Février 1983
Le site d'où est extraite l'image ci-contre ( anglais ) ICI

Le questionnaire interactif de Jacques Nimier : ICI

En ce qui me concerne C1: 0 C2: 2 C3: 4 C4: 6, vous verrez à quoi cela correspond à la dernière étape.

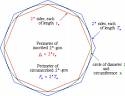La méthode d'exhaustion était utilisée par les mathématiciens grecs pour déterminer une longueur, une aire ou un volume. On pense à tort qu'elle est seulement constituée  par un "encadrement" d'une courbe par deux lignes brisées situées de part et d'autre, d'une surface par des polygones  ou d'un volume par des polyèdres, ceux-ci étant intérieurs et extérieurs. Ainsi, en " rapprochant " les objets créés de celui dont on cherche à évaluer la longueur, l'aire ou le volume, on aboutit intuitivement à un encadrement de la quantité cherchée.
La méthode d'exhaustion est en fait essentiellement constituée par la preuve irréfutable de cette intuition et la validation du résultat obtenu par une double réduction à l'absurde. C'est ce que nous explique à merveille André Ross dans un article ( PDF ) : ICI

Archimède utilisa cette méthode afin d'obtenir des résultats très originaux, dont un calcul d'aire faisant intervenir un " levier " pour comparer l'aire d'un triangle et l'aire d'un segment de parabole : ICI

Le résultat le plus connu est obtenu par Archimède, et est sans conteste, l'encadrement de Pi : ICI

Cette méthode, près de 2000 ans auparavant, préparait le terrain du calcul différentiel et intégral qui permettra des calculs plus généraux.

Cavalieri emprunta le chemin de ses ainés dans son Traité des indivisibles pour effectuer des calculs d'aire et de volume : ICI

La méthode de Descartes était purement algébrique, elle ne faisait pas intervenir les concepts de limite et d'infinitésimal,  la route se poursuivit avec Newton et Leibnitz et la naissance du calcul différentiel et intégral.

Pour info, voilà l'adresse de la page d'André Ross avec tous les articles cités et d'autres encore : ICI
Et d'autres articles d'André Ross : ICI

 

La perspective est sans doute le domaine où les mathématiques ont montré leur face la plus artistique. Dans un article ( PDF ) nommé "L'histoire de la perspective au XXème siècle: une déconstruction": ICI , Jeanne Peiffer interroge  les liens unissant ces deux aspects de la perspective, l'un mathématique, l'autre artistique. Celle-ci ne se laissant pas facilement enfermer dans l'un ou l'autre de ces deux domaines, J. Peiffer nous emmène aux sources de l'origine, entre mythe et métaphore, certitudes et inventions.

 

Si vous avez fait votre choix entre perspective mathématique ou perspective artistique, il faut maintenant passer aux travaux pratiques !
Pour construire une maison tout en douceur sur de la musique classique en perspective à un, puis deux, puis trois points :