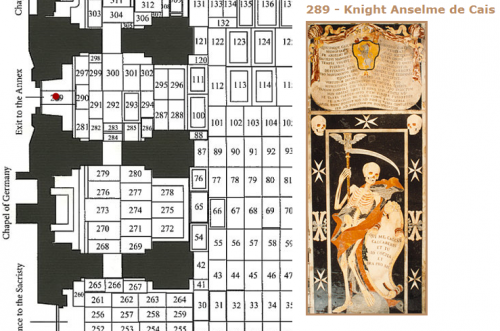
Qui me calcas calcaberis et tu id cogita et ora pro me
On va dire que le rapport avec les maths c'est le numéro des tombes... Je viens de les retrouver ces magnifiques tombes en marqueterie de marbre de la Co-Cathédrale Saint-John à Malte et celle que je préfère se situe à l'entrée, elle porte le numéro 289. C'est celle du chevalier Anselme de Cais sur laquelle est inscrite cette insciption latine :
Qui me calcas calcaberis et tu id cogita et ora pro me.
Ce qui veut dire en gros:
Toi qui me marche dessus, on te fouleras, penses-y et prie pour moi.
Cliquez sur l'image pour visiter les tombes de la Cathédrale, cliquez sur le plan bordeaux, puis déplacez le plan blanc avec la main. Cliquez ensuite sur une tombe puis faites passer votre souris sur l'image pour agrandir. Mais c'est quand même mille fois plus beau en vrai!
Et puisque vous me prenez par les sentiments, voilà une petite énigme:
Combien y a t il de crânes, au total, représentés sur les tombes portant les deux nombres (différents de 1) ayant la propriété suivante ?
La somme des cubes de mes chiffres est égale à un nombre dont la somme des cubes des siens m'est égale.