Le phénomène "Angry Birds"
Je vois passer depuis quelques temps dans mon lecteur de flux RSS, des articles vantant les mérites du jeu de type plateforme, "Angry Birds", qui posséderait les peu miscibles caractéristiques d'être d'une part addictif et d'autre part sérieux (au sens où le fait de jouer procurerait des bénéfices intellectuels).
Je ne suis pas un adepte des jeux mais par la force des choses et des messages répétés, j'ai fini par céder à la curiosité... et mener ma propre enquête.
Le principe du jeu
L'idée de base est de lancer des oiseaux grincheux avec un lance-pierres ( il y a un petit coté pas gentil mais comme c'est un jeu...) sur d'autres oiseaux dans des nids des petits cochons verts vus de face (qui ont l'air gentils eux). Le problème c'est que parfois ces oiseaux cochons sont protégés (et parfois très bien) par des structures. Il faut donc les faire s'écrouler. De plus certains oiseaux-projectiles sont à fragmentation et peuvent se décomposer en trois en cours de vol, d'autres mangent le bois et pour le reste je ne suis pas allé assez loin dans le jeu.
En gros ça donne ça :
Est-ce un jeu pédagogique ?
Je cite Fais-moi jouer :
Quelle est la méthode employée par le joueur pour progresser (pas nécessairement de manière complètement consciente) ?
Cette méthode est précisément la méthode hypothético-déductive utilisée par les sciences, théorisée au 20e siècle et que les enseignants s’échinent à inculquer aux élèves. Alors faut-il faire entrer Angry Birds dans les salles de classe ?
Il ne me semblait pas que c'était exactement cela la méthode hypothético-déductive.... car je ne vois pas bien ici la formulation d'une quelconque hypothèse. De plus la démarche scientifique ne serait pas nécessairement consciente! Tiens, tiens... Monsieur Jourdain fait de la prose sans le savoir.
Personnellement, je dirai plus que l'on utilise une méthode par essais-erreurs, ou un peu plus directement la méthode dite du bidouillage-réglage au pif. D'ailleurs si le résultat de ce jeu était lié aux capacités mathématiques, vous n'auriez pas constaté le triste résultat précédent!
Ce jeu n'est donc pas "pédagogique au sens de la démarche scientifique énoncée plus haut.
Mais peut-on pour cela conclure sur le fait que ce jeu ne contient aucune composante "pédagogique"?
Je pense en fait qu'il contient, hormis le fait que les garçons ont toujours révé de chasser avec un lance-pierres ( j'en fais partie), une expérimentation intéressante de la balistique et la découverte de la trajectoire parabolique avec les courbes possibles. Il s'avère donc que ce jeu réalise un travail assez intéressant et il est vrai ludique sur l'intériorisation de la forme possible d'une parabole. La connaissance de cette courbe m'a été d'un assez grand avantage pour jouer, mais encore faut-il que le lien soit fait entre la trajectoire de l'oiseau et la forme de la courbe vue en cours (en seconde). Il est aussi à noter que le jeu n'augmente pas vraiment les capacités à "étudier scientifiquement" ce genre de courbe.
On trouvera une activité scolaire sur la trajectoire parabolique avec GeoGebra ICI, l'objectif de l'exercice étant de savoir si le début de la représentation d'une trajectoire d'un ballon de basket est une trajectoire possible et si le ballon parviendra au panier.

On trouvera aussi dans le genre "animation GeoGebra ludique", le simple et excellent canon à poulets qui a sans doute inspiré l'auteur du jeu.
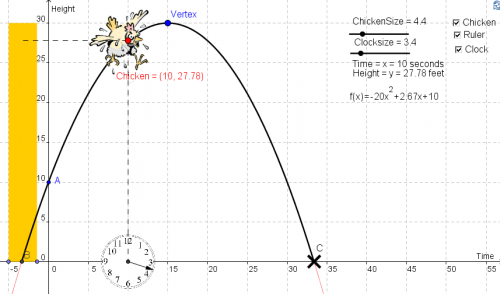
Si l'on sent le frémissement d'un jeu sérieux, je pense que le jeu dit "sérieux et pédagogique" permettrait à ce que des trajectoires de formes différentes puissent être par exemple utilisées soit dans des univers séparés soit par différents oiseaux dans un même univers. On pourrait ainsi concevoir des oiseaux à trajectoire carrée, cubique, linéaire, logarithmique, hyperbolique, valeur absolue ou exponentielle rendant le jeu encore plus intéressant mais aussi plus "pédagogique" au sens où il obligerait de se poser la question des différentes variations de fonctions de natures très différentes.
Mais que cela ne nous empèche pas de jouer... Angry Birds est installable gratuitement sur Chrome. J'en suis au tableau 19 et vous?
Nous jouions à la guerre des étoiles avec Space Invader et maintenant il jouent au lance-pierres à la campagne avec Angry Birds. Les temps changent!
Pour compléter : Thot Cursus