Prenez 1
Prenez 1

Additionnez les deux termes précédents et vous obtenez 2

Recommencez l'opération et vous obtenez 3 (= 2 + 1)  puis 5 (= 2 + 3 ) puis 8 puis 13 puis 21 puis 34....

C'est la suite de Fibonnacci

Faites les quotients de 2 termes consécutifs, le plus grand sur le plus petit, on obtient :

1/1 ; 2/1 ; 3/2 ; 5/3 ; 8/5 ; 13/8 ; 21/13 ; 34/21; ...

Et alors ?


Les termes de cette suite tendent inexorablement vers le nombre d'or ( environ 1,618 003 99...).

Et où trouve t-on le nombre d'or ?

Sur les jolis tableaux de peinture ( Le corbusier Le Modulator, Botticelli la naissance de Vénus, Raphael La vierge à l'enfant, Monet, La gare Saint Lazare, etc,etc )

Dans les belles figures de la nature ( l'oursin, l'étoile de mer, les coquillages, l'ananas, la pomme de pin, le bambou, les feuilles, les écailles, les pétales...), en fait il est souvent lié au principe de croissance.

Dans la belle musique avec le violon.

Je vous laisse approfondir les recherches si le coeur vous en dit...

Paradoxe de la corde prise au hasard ( Bertrand )

Problème : On trace une corde au hasard dans un cercle. Quelle est la probabilité pour que sa longueur soit supérieure au côté du triangle équilatéral inscrit ?

Bertrand donne 3 solutions différentes à ce problème.

En vert les cordes possibles

En rouge les cordes impossibles

Première solution :

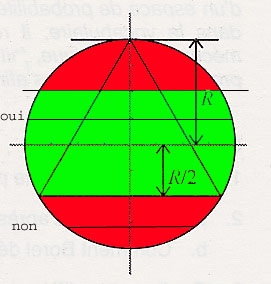
On peut pour des raisons de symétrie se donner la direction de la corde ; le point d'intersection de cette corde avec le diamètre ( vertical sur la figure ) perpendiculaire à cette direction  devra alors se trouver sur un segment  égal  à la moitié de la longueur de ce diamètre ( car la distance au centre du côté du triangle équilatéral inscrit est égale à la moitié du rayon ) ; la probabilité est donc de 1/2.

Deuxième solution :

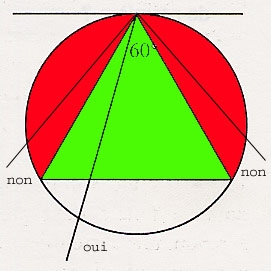
On peut, pour des raisons de symétrie, se donner une des extrémités de la corde sur le cercle ; la tangente en ce point et les 2 cotés du triangle équilatéral inscrit ayant ce point pour sommet forment trois angles de 60° ; la direction de la corde doit être à l'intérieur de l'angle formé par le triangle ( en vert) ; la probabilité est donc de 1/3.

Troisième solution :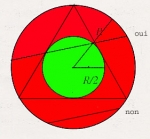

Pour fixer la position de la corde, il suffit de donner son milieu ; pour que la corde satisfasse à la condition de l'énoncé, il faut que son milieu soit intérieur à un cercle concentrique au cercle donné et de rayon moitié. La surface de ce cercle ( vert ) est le quart de la surface donnée ; la probabilité est donc de 1/4.

Doit-on penser que ces trois solutions sont également bonnes et, par suite, également mauvaises ? se demande Emile Borel dans son livre Le hasard parut en 1914. Nullement, poursuit-il, il s'agit simplement de préciser le mode d'après lequel se fera la vérification expérimentale, c'est à dire comment on s'y prendra pour tracer une corde au hasard : si on assujetit cette corde à passer par un point fixe du cercle ou si l'on fixe son milieu au hasard, il faudra choisir la deuxième ou la troisième solution, mais il est aisé de voir que la plupart des procédés naturels que l'on peut imaginer conduisent à la première.


Un site traite de ce "paradoxe" et permet la simulation des expériences : ICI

Un fichier pdf de Culturemath : ICI

Au début, c'est un carré

Puis un rectangle

Par la diagonale,

Deux triangles

Rectangles se séparent

lls deviennent quelconques

En six segments se défont

Vite des pointillés apparaissent

Laissant au loin de nombreux points

Enfin, une trace, légère

Presque sale.

J'ai trouvé sur un blog :

Comment prouver que tout ce qu'on dit est vrai ?

Un petit sophisme à résoudre. 

1. Ce que je veux dire est ce que j'ai l'intention de dire

2. J'ai l'intention de dire la vérité

3. Donc ce que je veux dire est vrai.

En terme d'étude de sophisme le sujet me parait très interessant.
L'approche philosophique de Gödel me semble capitale pour éclaircir le sujet ( l'ensemble des vérités ne coincide pas avec l'ensemble des démontrables )
Cela concerne aussi, à mon avis, un grand sujet philosophique sur l'humanité faisant des ravages incommensurables : que les gens croient  lorsqu'ils parlent  que c'est nécessairement une vérité qu'ils énoncent. A méditer...