Preuves sans mots...
Avez-vous des exemples de preuves sans mots comme l'illustration suivante, que je trouve excellente?

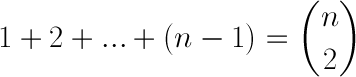
A chaque couple de la dernière ligne correspond un unique point jaune... d'où le résultat.
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies. Ces derniers assurent le bon fonctionnement de nos services. En savoir plus.
Avez-vous des exemples de preuves sans mots comme l'illustration suivante, que je trouve excellente?

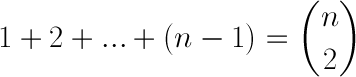
A chaque couple de la dernière ligne correspond un unique point jaune... d'où le résultat.
Je n'ai pas trouvé de traduction en français pour un triangle possédant un angle de 60°.
Un peu comme le triangle rectangle qui dispose de l'un des théorèmes les plus beaux des mathématiques, le triangle eutrigone, dont l'angle de 60° remplace celui de 90°, possède une propriété très analogue.
Si l'on trace des triangles équilatéraux sur chacun des cotés du triangle eutrigone, son aire est égale à la somme de celles des deux triangles adjacents à l'angle de 60° moins l'aire du troisième!
Belle propriété non?
Vous trouverez l'applet GeoGebra pour constater la propriété ICI.
Pour la démonstration, elle est du niveau de première S !
The area of an equilateral triangle with side
is
. By the law of sines, the area of a eutrigon is
. The law of cosines gives
, because
. Multiplying by
gives the statement of the theorem.
Voir le site de Wolfram.
 Certains mathématiciens refusent l'idée que l'infini puisse être un concept que l'on peut utiliser. Ce sont les finitistes. Les plus radicaux d'entre eux sont les ultrafinitistes dont faisait partie le mathématicien russe Alexander Yessenin-Volpin, logicien et poète ( qui a été interné dans un hopital psychiatrique en 1949 pour "poésie anti-soviétique" !).
Certains mathématiciens refusent l'idée que l'infini puisse être un concept que l'on peut utiliser. Ce sont les finitistes. Les plus radicaux d'entre eux sont les ultrafinitistes dont faisait partie le mathématicien russe Alexander Yessenin-Volpin, logicien et poète ( qui a été interné dans un hopital psychiatrique en 1949 pour "poésie anti-soviétique" !).
Lorsqu'on lui demandait si toutes les puissances de 2 avaient un sens, il précisait que la question devait être détaillée pour qu'il puisse y répondre et que chacun de ces nombres devait être étudié.
Il répondait presque instantanément que 21 était un réel. Lorsqu'on lui demandait si 22 était un réel, il mettait un peu plus de temps à répondre, puis encore plus de temps pour préciser que 23 en était aussi un. Et si on lui demandait un jour si 2100 était un réel, il mettrait 2100 plus de temps à répondre que pour 21. Belle façon de montrer qu'il était impossible de répondre à la question et que l'infini est un concept qui n'a pas de sens.
Source: L'excellent livre "Au nom de l'infini" de Cantor et Graham

 J'ai adoré ce livre de 188 pages aux illustrations fournies, alors qu'il ne m'était pas destiné. En effet l'auteur Rob Eastaway explique qu'il a écrit ce livre pour répondre à une journaliste qui mettait en doute la beauté des maths.
J'ai adoré ce livre de 188 pages aux illustrations fournies, alors qu'il ne m'était pas destiné. En effet l'auteur Rob Eastaway explique qu'il a écrit ce livre pour répondre à une journaliste qui mettait en doute la beauté des maths.
Le sous-titre du livre, très bien traduit par Olivier Courcelle, indique avec pertinence qu'il abordera les mathématiques surprenantes de la vie quotidienne, alors qu'en conclusion Rob remercie deux amis mathophobes, qui lui ont permis de savoir ce qu'il NE FALLAIT PAS mettre dans un livre comme celui-ci. Il est à noter que le livre ne perd rien en rigueur explicative mais gagne fortement en adoptant toujours un angle d'attaque favorable au lecteur qui n'est pas accomodé aux subtilités mathématiques.
Je connaissais de nombreuses propriétés citées, et malgré le fait que je baigne dans l'univers mathématique quotidiennement, je me suis fait encore surprendre par ses fascinantes propriétés, et j'ai encore découvert quelques merveilleux joyaux qui peuvent facilement s'énoncer. Je n'hésiterai d'ailleurs pas à présenter à l'occasion, à mes élèves, quelques propriétés amusantes telles que le paradoxe de Penney, qui donne un avantage décisif à celui qui débute dans un certain jeu de pile ou face ou celui du dictateur qui, pour soutenir une politique nataliste en faveur des garçons interdit aux mères ayant eu une fille, d'avoir un autre enfant... Politique paradoxalement d'un effet nul sur la répartition des naissances!
Je vous encourage donc à croquer dans ce petit moment de maths abordables, sous l'angle du AAHH (la beauté), du AHA (l'émerveillement) et du HAHA (le rire!).
Et, pour conclure... Si on a deux couleurs de chaussettes dans un tiroir, combien faut-il prélever de chaussettes au hasard (il fait noir le matin..), pour être certain d'avoir une paire de chaussettes de la même couleur? Et que se passe-t-il avec 3,4,5 puis n couleurs de chaussettes dans le tiroir?
Les diagrammes suivants, bien que très usuels m'ont posé pas mal de difficultés pour les insérer dans une publication numérique. Entre solutions longues et parfois bancales, je jonglais plus ou moins habilement avec les logiciels dont je disposais et des copies d'écran pas toujours de bonne qualité.
Pour réaliser ces diagrammes, il suffit d'installer PstPlus de le configurer correctement comme c'est expliqué. Attention, il faut indiquer pour Windows, le chemin de gswin32c.exe et non de gswin32.exe associé à Ghostscript. Il faut aussi installer une distribution Latex.
Une fois ces opérations réalisées, on peut générer un fichier en .eps à partir des différents assistants.
Il suffit ensuite d'utiliser un convertisseur en ligne pour obtenir une image. Pour ma part j'ai utilisé epsconverter, très facile d'emploi.