Paradoxe de la corde prise au hasard ( Bertrand )
Problème : On trace une corde au hasard dans un cercle. Quelle est la probabilité pour que sa longueur soit supérieure au côté du triangle équilatéral inscrit ?
Bertrand donne 3 solutions différentes à ce problème.
En vert les cordes possibles
En rouge les cordes impossibles
Première solution :
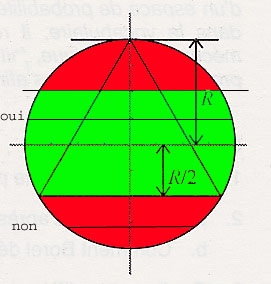
On peut pour des raisons de symétrie se donner la direction de la corde ; le point d'intersection de cette corde avec le diamètre ( vertical sur la figure ) perpendiculaire à cette direction devra alors se trouver sur un segment égal à la moitié de la longueur de ce diamètre ( car la distance au centre du côté du triangle équilatéral inscrit est égale à la moitié du rayon ) ; la probabilité est donc de 1/2.
Deuxième solution :
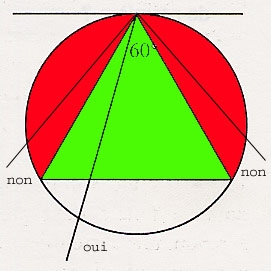
On peut, pour des raisons de symétrie, se donner une des extrémités de la corde sur le cercle ; la tangente en ce point et les 2 cotés du triangle équilatéral inscrit ayant ce point pour sommet forment trois angles de 60° ; la direction de la corde doit être à l'intérieur de l'angle formé par le triangle ( en vert) ; la probabilité est donc de 1/3.
Troisième solution :
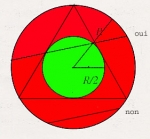
Pour fixer la position de la corde, il suffit de donner son milieu ; pour que la corde satisfasse à la condition de l'énoncé, il faut que son milieu soit intérieur à un cercle concentrique au cercle donné et de rayon moitié. La surface de ce cercle ( vert ) est le quart de la surface donnée ; la probabilité est donc de 1/4.
Doit-on penser que ces trois solutions sont également bonnes et, par suite, également mauvaises ? se demande Emile Borel dans son livre Le hasard parut en 1914. Nullement, poursuit-il, il s'agit simplement de préciser le mode d'après lequel se fera la vérification expérimentale, c'est à dire comment on s'y prendra pour tracer une corde au hasard : si on assujetit cette corde à passer par un point fixe du cercle ou si l'on fixe son milieu au hasard, il faudra choisir la deuxième ou la troisième solution, mais il est aisé de voir que la plupart des procédés naturels que l'on peut imaginer conduisent à la première.
Un site traite de ce "paradoxe" et permet la simulation des expériences : ICI
Un fichier pdf de Culturemath : ICI


