La catalogue général : ICI

La publication du CNRS " Images des mathématiques ", en fichiers PDF - extraits d'articles : ICI

Attention comme son nom ne l'indique pas il n'y a pas beaucoup d'images !

J'ai créé un nouveau Tag qui me faisait un peu défaut, celle des mathématiques dans leur fonction de science des modélisations et pour l'inaugurer j'y ai placé un site concernant le problème très médiatique du réchauffement climatique qui me parait extrémement solide et bien documenté : ICI

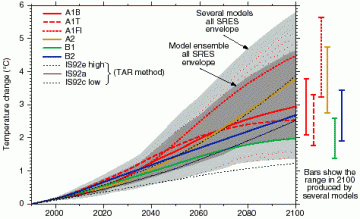
 En ce qui me concerne, j'ai une interprétation personnelle et à court terme du réchauffement climatique :
" Si réchauffement climatique il y a, plus de vents il y aura !".

Voilà un très beau site qui permet de mieux comprendre ce que sont les fractales et la récursivité : ICI

Parcourez le site, des galeries, des galeries dynamiques ou vous pouvez visualiser plus de 40000 fractales de façon aléatoire, des galeries dynamiques ou vous pouvez visualiser le caractère d'autosimilarité d'une fractale, des attracteurs et la possibilité de télécharger le logiciel de création ( l'interface est très rustique, je ne me suis pas encore penché dessus mais il me semble délicat à prendre en main en première approche ) : ICI