Les couvertures suivantes devraient suffire à vous convaincre d'aller ICI, où vous trouverez les revues au complet.

Et j'ai extrait cette photo ( revue mai 2007 ) que je trouve symboliquement belle :

Et voilà les résultats :

Le site de Bernar Venet : ICI

Ses expositions à Metz : ICI

Info trouvée ICI

La sculpture de la ligne B de Toulouse a été trouvée : ICI

Ligne indéterminée : ICI

De Saint-Nazaire à Bordeaux - Blog-O-Noisettes - des photos : ICI

Une belle photo à ne pas manquer : ICI

A Bordeaux, dans la rue, le blog de Xavier : ICI et le Portfolio : ICI

13 sculptures à Bordeaux : ICI

De belles photos en gros plan : ICI

Vernissage à l'Arsenal : ICI

La complexité mathématique de cet art japonais ancestral est de savoir si étant donné le tracé de plis sur une feuille de papier, celle-ci se pliera effectivement avec des formes planes localement, sans l'apparition d'autre pli. C'est ce qu'indique Ian Stewart pour introduire la naissance d'une nouvelle forme d'Origamis d'origine mathématique , "le Pinecone ".

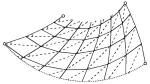
Dans le diagamme précédent, les lignes continues doivent être interprétées comme des arêtes et les pointillés comme des creux ( ou vallées).

C'est presque la même structure ( mais pas la même) que l'on retrouve fréquemment en phyllotaxie.

L'intégralité de l'article sur la page "Math in the media" de l'American Mathematical Society : ICI