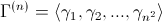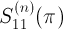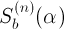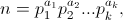Je vous conseille fortement la lecture du livre Poincaré écrit par Xavier Verley dont est extrait la citation suivante:

La recherche d'un fondement logique apparaît donc au moment où les mathématiques deviennent tellement abstraites qu'elles perdent tout lien avec la réalité : d'où la nécessité de les fonder en montrant que si elles s'éloignent de la réalité, elles retrouvent un lien avec la vérité ; mais la seule vérité qu'elles puissent alors atteindre est la vérité comme non-contradiction ou identité.

Ce qui est bien avec les matheux, c'est qu'ils s'amusent avec pas grand chose... Donnez leur des cercles et des carrés, et ils vous créent des problèmes difficiles que certains considèrent même ludiques. Les autres resteront à tout jamais fermés à cet amusement de l'esprit ou tout du moins au fait que le terrain de jeu puisse être amusant.

Pour commencer à  "s'amuser", nous (pas moi mais J. Ricardo Mendoça) pouvons définir une nouvelle catégorie de nombres basés sur la première occurrence d'un certain motif de 0 et de 1 apparaissant dans le développement d'un nombre irrationnel dans une base donnée et les appeler "Nombres de Sagan" en référence à la première fois où de tels nombres ont été mentionnés par l'astronome américain Carl E. Sagan dans le roman de Science-Fiction Contact.

Pour débuter il faut définir la notion de n-cercle digital.

Définition du n-cercle digital.

Un n-cercle digital noté:

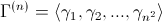
est une chaîne de n² bits, γi= 0 ou 1 qui assemblés de la gauche vers la droite et du haut vers le bas  codent un cercle digitalisé de diamètre n.

Il existe plusieurs façons de procéder. La deuxième approche "minimaliste" sera préférée, dans laquelle le nombre de 1 est minimal plutôt utilisée dans les technologies graphiques et les algorithmes qui donne le graphique (b).

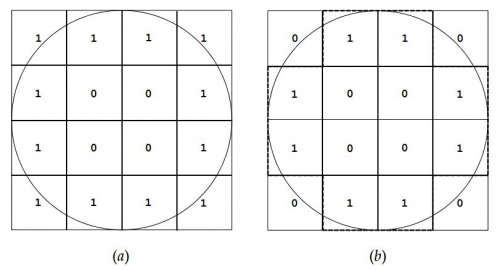
On obtient les figures suivantes:

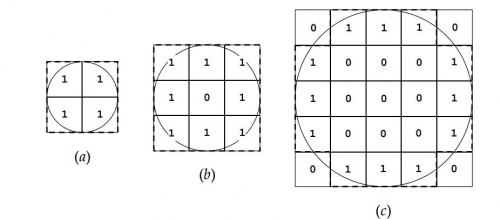
Ainsi:

On peut maintenant définir ce qu'est un nombre de Sagan.

Définition des nombres de Sagan.

Le n^ième nombre de Sagan décimal est la position dans la partie fractionnaire du développement de  π  en base 11, du premier chiffre du motif du n-cercle digital. On le note:

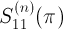
Les nombres de Sagan peuvent être généralisé pour n'importe quel nombre irrationnel  α et n'importe quelle base b. On les notera:

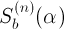
Et bien voilà, les présentations sont terminées et les matheux peuvent commencer à jouer afin de déterminer l'existence et la valeur de ces fameux nombres de Sagan! le problème posé touche du doigt la question de la normalité des nombres irrationnels dans n'importe quelle base, correspondant à l'équirépartition de chaque chiffre dans leur écriture.

Les premiers "chiffres" de Pi en base 11:

3.16150702865a48523521525977752941838668848853163a1a5421300465806522735053

3715271781a656371578133492888528191299206342527078127554826927697818064038

6187079590752454659a8876a29287267aa95754164754284475a718a59606a751a7513412

7a0525aa74070138624292a2542a3167921550550622029836612734698a08a2556602916a

53571454756894a25805a65a505a98131716aaa38868204098325970aaa553105877763582

301653133a753443a98119127676211a199730a1897918449a5a38659409534a4460107722

3546a614094a5809235096474789427705a3a4922410740916570038977533771952676361

38386036442694829545102839328755129856a85a524781730969a4080a901040093010a1

41a112654a8a9358a3a83415286a887a829645600582179834334013a419985988702a2549

a452143497638a92672a26203672a5216966415061384a077a389a3923102a21106200957a

6106554a8a54161713428538a39868214084a090107323154a7053692181190a04553706a6

51a3343816673a2892030896533aa225714357424631651155473011819a72362a78900493

8559a71067133093a7264a741886685073a93970747430aa68948218104271501328925862

5974765794718568955382a4423a30a2394278197543649849710aa0a9804...

Le premier nombre de Sagan est donc 1.
Il faut ensuite trouver la première occurrence de 1111 dans la liste (incomplète) précédente qui doit certainement se trouver entre les positions 10000 et 20000
Etc... 

De quoi occuper de longues soirées d'hiver d'un matheux en quête d'amusement.

Source: Sagan Numbers - Arxiv - J. Ricardo G. Mendonça (document avec exercices!)

Il semble qu'aujourd'hui le nombre 2 soit considéré comme le plus petit nombre premier. Mais cela n'a pas toujours été le cas. Il y a eu des temps et des mathématiciens, jusqu'à une période récente, pour lesquels les nombres 1 et 3 étaient une réponses acceptable.

Il est possible de dire que la problématique du plus petit nombre premier a été tranché lorsqu'ils ont été liés à l'unicité de la factorisation des nombres. Cette unicité est apportée par l'insertion des deux symboles "1<" dans le théorème suivant:

Pour chaque entier naturel n, il existe une unique factorisation
                                 
où les exposants a_i  sont des entiers positifs et 1<p₁<p₂<…<p_k  sont des nombres premiers.

Mais avant cela, pendant plus de deux millénaires, la liste des nombres premiers ne commençait pas toujours par 2.

Lorsque 1 n'était pas considéré comme un nombre, il était légitime que 2 soit le premier nombre nombre premier (Euclide).... sauf dans le cas où l'ensemble des nombres premiers était considéré comme un sous-ensemble des nombres impairs (Martianus Capella)- vers 420) mais cela ne l'était plus lorsque 1 devenait un nombre au même titre que les autres, puisqu'il était possible de l'utiliser dans les opérations arithmétiques et pour mesurer (Stevin - 1585).

Sans réflexion approfondie sur la primalité du nombre 1, une longue période de confusion allait naître.

On trouve par exemple dans cette lettre de Goldbach à Euler, l'écriture des entiers comme somme de nombres premiers, dont 1.

Gauss ne donna pas de définition explicite des nombres premiers mais participa à considérer la factorisation comme un élément central.

Cependant, après Gauss, de nombreux mathématiciens continuèrent à placer le nombre 1 dans la liste des nombres premiers et donc à la considérer comme le plus petit d'entre eux. On trouvera des noms célèbres tels que Legendre (1853), Weierstrass, Klein, Kronecker, Chebychev, Landau (1909). 

On peut se demander quel fut le dernier mathématicien à placer 1 dans la liste des nombres premiers.  

Et le gagnant n'est pas tout à fait "inconnu" et c'est en 1933 lors de la sixième version de " A course of Pure Mathematics" que l'on voit apparaître pour la dernière fois le nombre 1 comme plus petit nombre premier.

Dans la septième édition en 1938, le texte est modifié et la liste des nombres premiers commence par 2.

Source:  What is the smallest prime? Arxiv Caldwell et Xiong

A voir, ne serait-ce que pour la présentation colorée de ce monument des mathématiques.

http://www.geogebratube.org/material/show/id/13144