Nom d'un théorème !
Souvent le découvreur ou le diffuseur d'un théorème est éponyme. Qui ne connaît pas le théorème de Thalès ou de Pythagore? Mais certains théorèmes possèdent des noms assez surprenants. J'en ai trouvé quelques uns, mais pas énormément comme je l'aurai pensé initialement. Une explication en langue usuelle est donnée dans chacun des cas. Les mathématiques sous-jacentes à l'énoncé de ces théorèmes ne sont pas toutes simples, et je ne doute pas que le spécialiste se documentera sur la question. Si vous en connaissez d'autres, ils seront les bienvenus...
Il est très connu des élèves de lycée. Lorsque l'on est entre deux gendarmes et qu'ils se dirigent vers le même endroit, on n'a pas d'autre choix que d'y aller aussi.
Photo: www.ahgv.ch
Il est aussi très connu des élèves de lycée. Deux plans sécants de l'espace représentent le toit en question et l'intersection le faitage. Deux droites parallèles incluses respectivement danschacun des deux plans, comme par exemple des goutières, sont parallèles au faitage ( à la droite d'intersection des deux plans ).
Photo: Édouard BERGÉ
 Le théorème des restes chinois
Le théorème des restes chinois
D'un niveau bien plus élevé que les précédents, il est ainsi nommé car il permet de répondre à la question suivante : Combien l'armée de Han Xing comporte-t-elle de soldats si, rangés par 3 colonnes, il reste deux soldats, rangés par 5 colonnes, il reste trois soldats et, rangés par 7 colonnes, il reste deux soldats ?
Photo : Laurent van Roy
Si l'on décide de paver un plan avec des polygones identiques, l'hexagone régulier est celui qui a le plus petit périmètre. Pas bête la guèpe... euh l'abeille!
Photo: Jean-Etienne Poirrier
 Le théorème des mariages
Le théorème des mariages
G désigne un ensemble de garçons, F désigne un ensemble de filles, et f est l'application qui à chaque garçon associe l'ensemble des filles qui lui plaisent. Alors, si pour chaque sous-groupe de garçons, l'ensemble des filles qui leur plaît est plus grand que le nombre de garçons de ce sous-groupe, on peut marier chaque garçon à une fille différente qui lui plaît.
Jean-Eugène Buland
 Le théorème de la boule chevelue
Le théorème de la boule chevelue
Intuitivement, on peut se représenter une sphère recouverte de cheveux souples et pas frisés, chaque point de la sphère étant la racine d'un cheveu. On considère la projection du cheveu sur le plan tangent à la sphère au point où le cheveu pousse : l'ensemble de ces projections donne une bonne idée d'un champ de vecteurs tangents sur la sphère. On cherche alors à coiffer ces cheveux en les aplatissant sur la surface de la boule, et en évitant les discontinuités: on ne fait pas de raie, on ne permet pas à des cheveux de changer brutalement de direction les uns par rapport aux autres. Le théorème dit que c'est impossible d'arriver à ce résultat. Quoi qu'on fasse, on va causer la formation d'au moins un épi, c'est-à-dire d'un endroit où un cheveu se dressera.
Le théorème des quatre couleurs
Les mathématiciens aiment colorier. Peut-être n'ont-ils pas eu le temps de le faire à l'école, alors ils rattrapent le temps perdu.
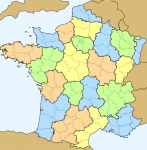
Dès 1852, l'un d'entre eux se demanda combien il fallait de couleurs pour colorier tous les pays de n'importe quelle carte sans que deux pays voisins n'aient la même couleur. Le problème est capital car dans le cas contraire on ne pourrait plus distinguer ces deux pays après coloriage. Il pensa que quatre devait être suffisant. Beaucoup de mathématiciens prirent aussi leurs crayons de couleurs et se mirent d'accord sur le nombre : 4 doit convenir mais ils ne s'accordèrent qu'à moitié sur la preuve car celle-ci faisait intervenir un bien étrange "personnage": un ordinateur. Bref après quelques guéguerres internes sur le style, l'incontournable boite aux quatre crayons nécessaire pour colorier toutes les cartes planes imaginables de l'univers s'appelle désormais "Théorème des quatre couleurs".
 Théorème du sandwich au jambon
Théorème du sandwich au jambon
On peut toujours trancher (selon un plan) un sandwich au jambon de façon à le partager avec la même quantité de chaque ingrédient.
 Le théorème des gendarmes
Le théorème des gendarmes Le théorème du toit
Le théorème du toit Le théorème du nid d'abeilles
Le théorème du nid d'abeilles