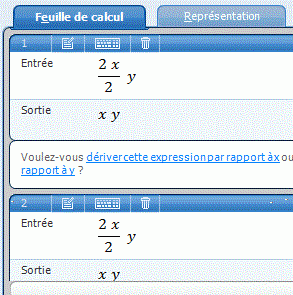
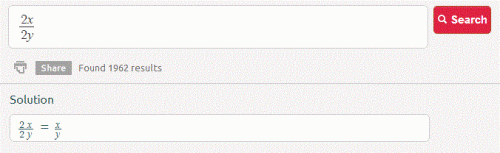
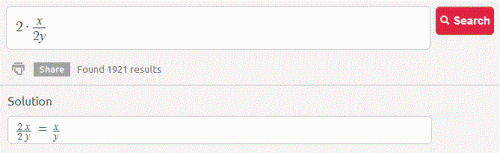
Est-ce que 2x/2y = 2*x/2*y ?
Alors que les professeurs de mathématiques sont souvent les gardiens du temple de la rigueur lorsque celle-ci fait défaut chez leurs élèves, la réponse à cette question simple ne semble pas faire l'unanimité dans les codes de calcul formel...
Il y a le camp des OUI et celui des NON ! C'est génant, non? N'hésitez pas à enrichir cette liste en commentaires.
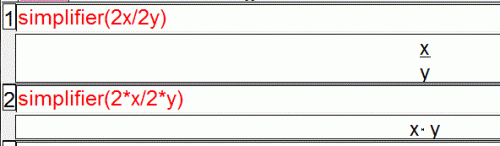
Chez les OUI on trouvera :
GeoGebra:
WIRIS:
WIMS
Microsoft Mathematics:
Maxima (dans Casyopée):
Symbolab (avec un résultat différent des précédents):
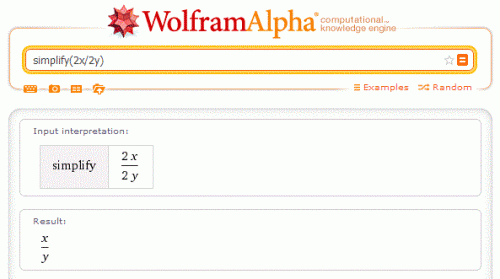
Chez les NON:
XCAS:
Wolfram Alpha:
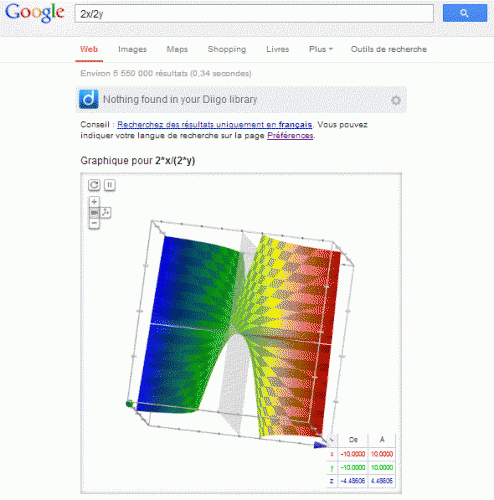
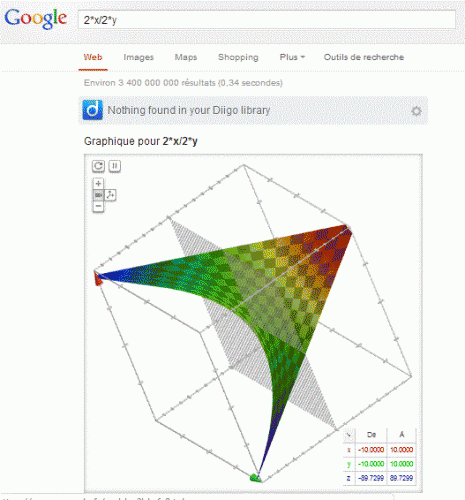
Google (représentation graphique de la fonction)

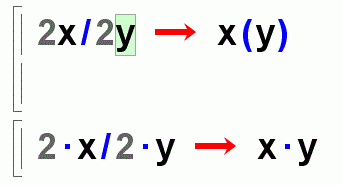



Commentaires
DERIVE donne le même résultat que Microsoft Mathématics
Bonjour,
A propos justment de l'utilisation potentielle des outils de calcul formel en classe, que penser des solutions proposées par ces logiciels de l'équation simpliste
exp(2 ln(x) - 3) = x
qui seraient exp(3)... et 0 !
Pas toujours facile de le gérer avec des élèves...
Alors la, je suis quelque peu pas d'accord avec B.Ray. Comment 0 peut il etre solution, alors qu'il ne fait pas partie de l'ensemble de definition. Une des premieres choses qu'on enseigne au eleves a propos de la fonction ln est qu'elle n'est definie que pour des nombres reelles STRICTEMENT plus grands que 0, donc 0 exclu.
En ce qui me concerne, a un niveau lycee, dire que 0 est solution de cette equation n'a aucun sens (pour ce qui est du post bac, je ne dis pas)
(Apres relecture du commentaire, j'ai l'impression qu'il peut etre interprete comme un peu aggressif, mais point du tout; c'est juste une petite remarque des plus amicales :) )
Cordialement
Les deux écritures sont maintenant cohérentes sur WolframAlpha.
"So now Mathematica / Wolpham Alpha are consistent with themselves, with PEMDAS, and with the TI-89, at least in regards to the evaluation of 2x/2y
- Juan"
Sur Mathfuture