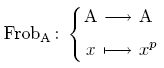Chine et mathématiques : des nouvelles fraîches
J'avais publié cette note " La Chine et les mathématiques " à l'occasion de l'ouverture des JO et les informations dataient un peu. Voilà une nouvelle beaucoup plus fraîche :
Géométrie algébrique : SUN Xiaotao fait d'importantes avancées
http://www.bulletins-electroniques.com/actualites/55632.htm
Avec l'aide d'une bourse des Jeunes boursiers d'élite de la Fondation Nationale des Sciences Naturelles de Chine(Distinguished Young Scholars of the National Natural Science Foundation of China), le Professeur Sun Xiaotao, de l'Académie des Sciences Chinoises pour les mathématiques et les sciences des systèmes (CAS Academy of Mathematics and Systems Science), a récemment réalisé une importante découverte en révélant une profonde relation entre la stabilité des vecteurs faisceaux et le morphisme de Frobénius. Ce travail est considéré comme très important et d'une grande valeur théorique.
La stabilité d'un vecteur faisceau est un des concepts fondamentaux en géométrie algébrique et a de multiples applications en mathématiques.
Le travail du Professeur Sun a été publié dans l'édition 2008 du journal Inventiones Matematicae sous le titre "Direct Images of Bundles under Frobenius Morphism". Son étude a attiré de nombreux mathématiciens connus mondialement. Le morphisme de Frobénius est la notation la plus fondamentale en géométrie algébrique de caractéristique positive. Le théorème du Professeur Sun révèle la relation entre la stabilité des images directes de Frobénius et la stabilité des faisceaux cotangents.
Source : Académie des Sciences Chinoise (Chinese Academy of Sciences - CAS) - http://english.cas.cn/eng2003/news/detailnewsb.asp?InfoNo=27244
Bien que le concept me dépasse un peu, il semble que cela soit rudement important !
Pour compléter : Corps finis